Graph Convolutions using Protein structures
This post shows how to implement a simple graph convolutional deep learning method to predict interfaces between protein residues, i.e. given a pair of interacting proteins, can we classify a pair of amino acid residues as interacting or not. This is based on the paper published in NIPS 2017 (Protein Interface Prediction using Graph Convolutional Networks).
The code and data here is a simplified and easy to understand version based on the published repository. My goal is to quickly introduce the readers to a deep learning architecture that uses graph convolutions without getting bogged down with the internals of protein structure. The full implementation of the things discussed below can be found at full code.
First I start with the description of the training data and then how we can build a graph convolutional model step by step using the data to solve the protein interface prediction problem. First load the training data ‘train.cpkl’ as :
import pickle
import os
#assumes train.cpkl is placed in a local directory 'data'.
train_data_file = os.path.join('./data/','train.cpkl')
train_list, train_data = pickle.load(open(train_data_file,'rb'),encoding='latin1')
print('No of molecules in Training = ', len(train_data))
molecule_pair = train_data[0]
print(molecule_pair.keys())
Output:
No of molecules in Training = 175
dict_keys(['l_vertex', 'complex_code', 'r_hood_indices', 'l_hood_indices',
'r_vertex', 'label', 'r_edge', 'l_edge'])
Here, the training data has 175 pairs of molecules. Each molecule-pair is a dictionary with 8 keys. It has entries for ‘ligand molecule’ denoted by “l_” and receptor molecule denoted by “r_”.
print("l_vertex = [%d,%d]"%(molecule_pair['l_vertex'].shape))
print("l_edge = [%d,%d,%d]"%(molecule_pair['l_edge'].shape))
print("l_hood_indices = [%d,%d,%d]"%(molecule_pair['l_hood_indices'].shape))
print('--------------------------------------------------')
print("r_vertex = [%d,%d]"%(molecule_pair['r_vertex'].shape))
print("r_edge = [%d,%d,%d]"%(molecule_pair['r_edge'].shape))
print("r_hood_indices = [%d,%d,%d]"%(molecule_pair['r_hood_indices'].shape))
print('--------------------------------------------------')
print("label = [%d,%d]"%(molecule_pair['label'].shape))
print(molecule_pair['label'][0:5,:])
Output:
l_vertex = [185,70]
l_edge = [185,20,2]
l_hood_indices = [185,20,1]
--------------------------------------------------
r_vertex = [362,70]
r_edge = [362,20,2]
r_hood_indices = [362,20,1]
--------------------------------------------------
label = [1683,3]
[[111 358 1]
[ 11 287 1]
[115 301 1]
[ 10 286 1]
[ 34 352 1]]
Thus for this molecule pair, the ligand molecule has 185 residues each with 20 neighbors (fixed in this dataset). The receptor molecule has 362 residues each with 20 neighbors again. The label indicates the +1/-1 status of every residue pair indicating whether the pair of residues are interacting(+1) or not(-1). Note that not all pairs of residues are present in the label as the authors have chosen to downsample the negative examples for an overall ratio of 10:1 of negative to positive examples. With this description, lets move onto define the placeholder tensors for building the graph convolutional network.
import tensorflow as tf
in_nv_dims = train_data[0]["l_vertex"].shape[-1]
in_ne_dims = train_data[0]["l_edge"].shape[-1]
in_nhood_size = train_data[0]["l_hood_indices"].shape[1]
in_vertex1 = tf.placeholder(tf.float32,[None,in_nv_dims],"vertex1")
in_vertex2 = tf.placeholder(tf.float32,[None,in_nv_dims],"vertex2")
in_edge1 = tf.placeholder(tf.float32,[None,in_nhood_size,in_ne_dims],"edge1")
in_edge2 = tf.placeholder(tf.float32,[None,in_nhood_size,in_ne_dims],"edge2")
in_hood_indices1 = tf.placeholder(tf.int32,[None,in_nhood_size,1],"hood_indices1")
in_hood_indices2 = tf.placeholder(tf.int32,[None,in_nhood_size,1],"hood_indices2")
input1 = in_vertex1, in_edge1, in_hood_indices1
input2 = in_vertex2, in_edge2, in_hood_indices2
examples = tf.placeholder(tf.int32,[None,2],"examples")
labels = tf.placeholder(tf.float32,[None],"labels")
dropout_keep_prob = tf.placeholder(tf.float32,shape=[],name="dropout_keep_prob")
The code implements the following network architecture :
ligand-residue --> ligand_graph_conv_layer1 --> ligand_graph_conv_layer2
|
--> merged --> dense1 --> dense2 --> prediction
|
receptor-residue --> receptor_graph_conv_layer1 --> receptor_graph_conv_layer1
So input1 will represent the input to the network containing information for ligand residue of the pair, analogously, input2 will represent the input to th network containing information for receptor residue of the pair. We will use the following function ‘node_average_model’ to perform the graph convolution (e.g. in ligand_graph_conv_layer1 and receptor_graph_conv_layer2) :
import numpy as np
def initializer(init, shape): #helper function to initialize a tensor
if init == "zero":
return tf.zeros(shape)
elif init == "he":
fan_in = np.prod(shape[0:-1])
std = 1/np.sqrt(fan_in)
return tf.random_uniform(shape, minval=-std, maxval=std)
def nonlinearity(nl): #helper function to determine the type of non-linearity
if nl == "relu":
return tf.nn.relu
elif nl == "tanh":
return tf.nn.tanh
elif nl == "linear" or nl == "none":
return lambda x: x
# the function that defines the ops for graph onvolution.
def node_average_model(input, params, filters=None, dropout_keep_prob=1.0, trainable=True):
vertices, edges, nh_indices = input
nh_indices = tf.squeeze(nh_indices, axis=2)
v_shape = vertices.get_shape()
nh_sizes = tf.expand_dims(tf.count_nonzero(nh_indices + 1, axis=1, dtype=tf.float32), -1)
# for fixed number of neighbors, -1 is a pad value
if params is None:
# create new weights
Wc = tf.Variable(initializer("he", (v_shape[1].value, filters)), name="Wc", trainable=trainable) # (v_dims, filters)
Wn = tf.Variable(initializer("he", (v_shape[1].value, filters)), name="Wn", trainable=trainable) # (v_dims, filters)
b = tf.Variable(initializer("zero", (filters,)), name="b", trainable=trainable)
else:
Wn, Wc = params["Wn"], params["Wc"]
filters = Wc.get_shape()[-1].value
b = params["b"]
params = {"Wn": Wn, "Wc": Wc, "b": b}
# generate vertex signals
Zc = tf.matmul(vertices, Wc, name="Zc") # (n_verts, filters)
# create neighbor signals
v_Wn = tf.matmul(vertices, Wn, name="v_Wn") # (n_verts, filters)
Zn = tf.divide(tf.reduce_sum(tf.gather(v_Wn, nh_indices), 1), tf.maximum(nh_sizes, tf.ones_like(nh_sizes))) # (n_verts, v_filters)
nonlin = nonlinearity("relu")
sig = Zn + Zc + b
h = tf.reshape(nonlin(sig), tf.constant([-1, filters]))
h = tf.nn.dropout(h, dropout_keep_prob)
return h, params
The equation behind the tensor operations in the above function ‘node_average_model’ are in
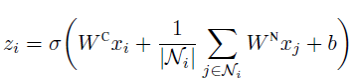
#layer 1
layer_no = 1
name = "ligand_graph_conv_layer1"
with tf.name_scope(name):
output, params = node_average_model(input1, None, filters=256, dropout_keep_prob=0.5)
input1 = output, in_edge1, in_hood_indices1
name = "receptor_graph_conv_layer1"
with tf.name_scope(name):
output, _ = node_average_model(input2, params, filters=256, dropout_keep_prob=0.5)
input2 = output, in_edge2, in_hood_indices2
#layer 2
layer_no = 2
name = "ligand_graph_conv_layer2"
with tf.name_scope(name):
output, params = node_average_model(input1, None, filters=256, dropout_keep_prob=0.5)
input1 = output, in_edge1, in_hood_indices1
name = "receptor_graph_conv_layer2"
with tf.name_scope(name):
output, _ = node_average_model(input2, params, filters=256, dropout_keep_prob=0.5)
input2 = output, in_edge2, in_hood_indices2
Note that the weights are shared between ligand_graph_conv_layer1 receptor_graph_conv_layer1. Similarly weights are shared between ligand_graph_conv_layer2 receptor_graph_conv_layer2. Next add the layers to merge the outputs from ‘ligand_graph_conv_layer2’ and ‘receptor_graph_conv_layer2’ - essentially concatenating the tensors along the feature dimension with both possible orders : (ligand,receptor) and (receptor,ligand).
# merged layers
layer_no = 3
name = "merged"
merge_input1 = input1[0]
merge_input2 = input2[0]
with tf.name_scope(name):
m_out1 = tf.gather(merge_input1, examples[:, 0])
m_out2 = tf.gather(merge_input2, examples[:, 1])
# concatenate in both possible orders : (ligand,receptor) and (receptor,ligand).
output1 = tf.concat([m_out1, m_out2], axis=0)
output2 = tf.concat([m_out2, m_out1], axis=0)
merged_output = tf.concat((output1, output2), axis=1)
Next add the two densely connected layers using the merged output. Define the function for the dense layer:
def dense(input, out_dims=None, dropout_keep_prob=1.0, nonlin=True, trainable=True):
input = tf.nn.dropout(input, dropout_keep_prob)
in_dims = input.get_shape()[-1].value
out_dims = in_dims if out_dims is None else out_dims
W = tf.Variable(initializer("he", [in_dims, out_dims]), name="w", trainable=trainable)
b = tf.Variable(initializer("zero", [out_dims]), name="b", trainable=trainable)
Z = tf.matmul(input, W) + b
if(nonlin):
nonlin = nonlinearity("relu")
Z = nonlin(Z)
Z = tf.nn.dropout(Z, dropout_keep_prob)
return Z
And connect it with merged_output:
# dense layer 1
layer_no = 4
name = "dense1"
with tf.name_scope(name):
dense1_output = dense(merged_output, out_dims=512, dropout_keep_prob=0.5, nonlin=True, trainable=True)
# dense layer 2
layer_no = 5
name = "dense2"
with tf.name_scope(name):
dense2_output = dense(dense1_output, out_dims=1, dropout_keep_prob=0.5, nonlin=False, trainable=True)
Add the final layer, essentially averaging the predictions from both orders of combinations. See
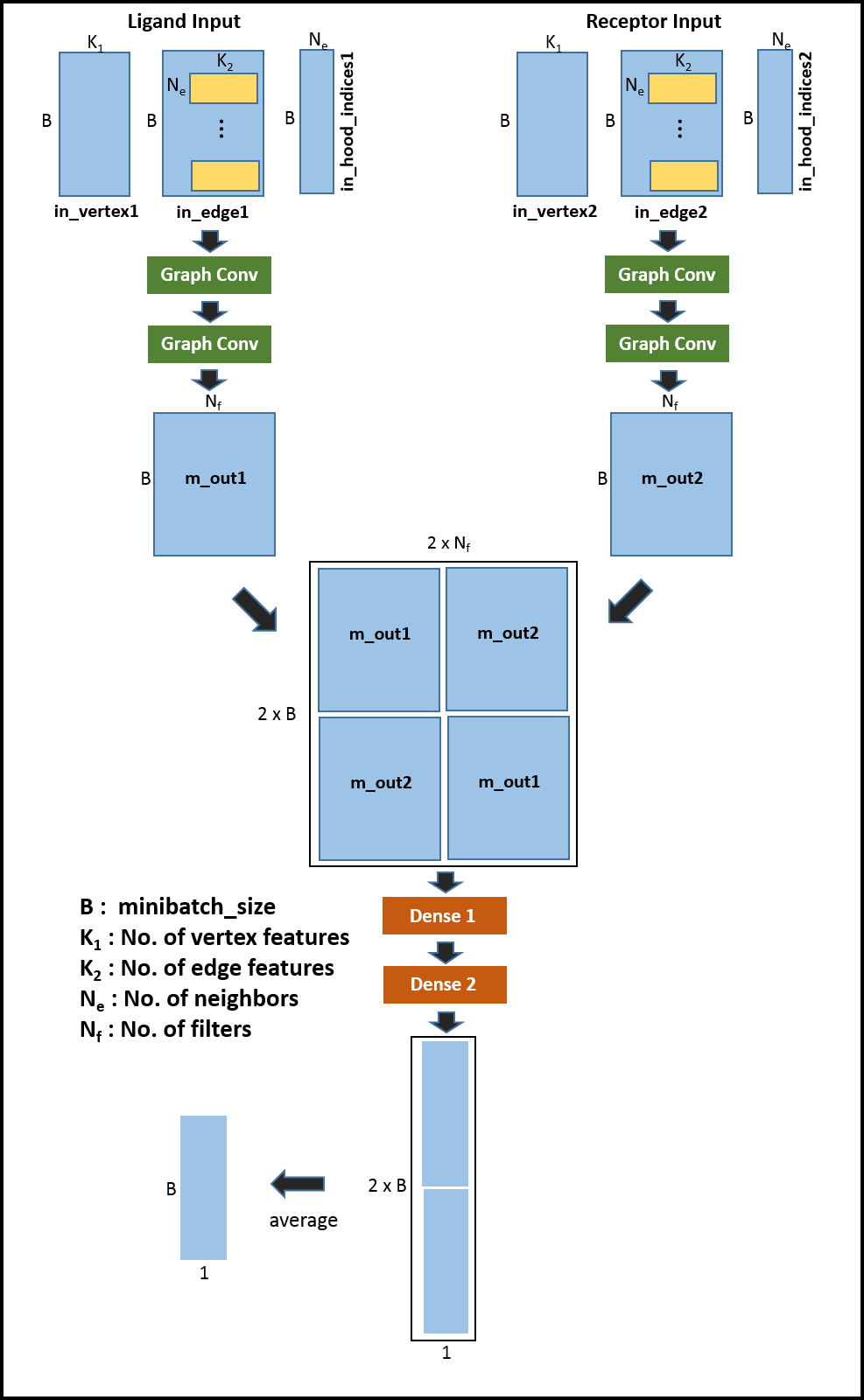
# add layer to get mean prediction across both the orders (ligand,receptor) and (receptor,ligand)
layer_no = 6
name = "do_prediction"
with tf.name_scope(name):
preds = tf.reduce_mean(tf.stack(tf.split(dense2_output, 2)), 0)
pn_ratio = 0.1
learning_rate = 0.05
#add loss op
# Loss and optimizer
with tf.name_scope("loss"):
scale_vector = (pn_ratio * (labels - 1) / -2) + ((labels + 1) / 2)
logits = tf.concat([-preds, preds], axis=1)
labels_stacked = tf.stack([(labels - 1) / -2, (labels + 1) / 2], axis=1)
loss = tf.losses.softmax_cross_entropy(labels_stacked, logits, weights=scale_vector)
with tf.name_scope("optimizer"):
# generate an op which trains the model
train_op = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
Now time for training the model, will do just one epoch. In practice, you will need to run more than 100 epochs to get reasonale test results.
def build_feed_dict(minibatch):
feed_dict = {
in_vertex1: minibatch["l_vertex"], in_edge1: minibatch["l_edge"],
in_vertex2: minibatch["r_vertex"], in_edge2: minibatch["r_edge"],
in_hood_indices1: minibatch["l_hood_indices"],
in_hood_indices2: minibatch["r_hood_indices"],
examples: minibatch["label"][:, :2],
labels: minibatch["label"][:, 2],
dropout_keep_prob: dropout_keep
}
return feed_dict
num_epochs = 1 #change this while real training.
minibatch_size = 128
dropout_keep = 0.5
sess = tf.Session()
sess.run(tf.global_variables_initializer())
print("Training Graph Conv Model ...")
for epoch in range(0, num_epochs):
"""
Trains model for one pass through training data, one protein at a time
Each protein is split into minibatches of paired examples.
Features for the entire protein is passed to model, but only a minibatch of examples are passed
"""
prot_perm = np.random.permutation(len(train_data))
ii = 0
nn = 0
avg_loss = 0
# loop through each protein
for protein in prot_perm:
# extract just data for this protein to create minibatches.
prot_data = train_data[protein]
pair_examples = prot_data["label"]
n = len(pair_examples)
shuffle_indices = np.random.permutation(np.arange(n)).astype(int)
# loop through each minibatch or ligand-receptor pairs for this protein.
for i in range(int(n / minibatch_size)):
# extract data for this minibatch
index = int(i * minibatch_size)
example_pairs = pair_examples[shuffle_indices[index: index + minibatch_size]]
minibatch = {}
#copy data to minibatch.
for feature_type in prot_data:
if feature_type == "label":
minibatch["label"] = example_pairs
else:
minibatch[feature_type] = prot_data[feature_type]
# train the model
feed_dict = build_feed_dict(minibatch)
_,loss_v = sess.run([train_op,loss], feed_dict=feed_dict)
avg_loss += loss_v
ii += 1
print(ii," Batch loss = ",loss_v)
nn += n
print("Epoch_end =",epoch,", avg_loss = ",avg_loss/ii," nn = ",nn)
One epoch of training gives:
Training Graph Conv Model ...
1 Batch loss = 0.112723
2 Batch loss = 0.118632
3 Batch loss = 0.125916
4 Batch loss = 0.162415
5 Batch loss = 0.117011
6 Batch loss = 0.112846
7 Batch loss = 0.135485
8 Batch loss = 0.119522
9 Batch loss = 0.112589
.
.
.
1285 Batch loss = 0.125246
1286 Batch loss = 0.136294
1287 Batch loss = 0.11121
1288 Batch loss = 0.118586
1289 Batch loss = 0.123084
Epoch_end = 0 , avg_loss = 0.125743936039 nn = 176044
import copy
from sklearn.metrics import roc_curve, auc, average_precision_score
all_preds = []
all_labels = []
all_losses = []
for prot_data in train_data:
temp_data = copy.deepcopy(prot_data)
n = prot_data['label'].shape[0] #no of labels for this protein molecule.
#split the labels into chunks of minibatch_size.
batch_split_points = np.arange(0,n,minibatch_size)[1:]
batches = np.array_split(prot_data['label'],batch_split_points)
for a_batch in batches:
temp_data['label'] = a_batch
feed_dict = build_feed_dict(temp_data)
res = sess.run([loss,preds,labels], feed_dict=feed_dict)
pred_v = np.squeeze(res[1])
if len(pred_v.shape)==0:
pred_v = [pred_v]
all_preds += pred_v
else:
pred_v = pred_v.tolist()
all_preds += pred_v
all_labels += res[2].tolist()
all_losses += [res[0]]
fpr, tpr, _ = roc_curve(all_labels, all_preds)
roc_auc = auc(fpr, tpr)
print('mean loss = ',np.mean(all_losses))
print('roc_auc = ',roc_auc)
Output :
mean loss = 0.121488
roc_auc = 0.569184936411
Looks awful, but this is testing after just one epoch of training. You will get much better results with more than 100 epochs of training.
