Markov Random Fields (MRF)
A short intro to MRFs. Let \( \textbf{X} =\{ X_1,X_2,…,X_n \} \) be a family of random variables defined on a set \( S=\{1,2,…,n\} \) of sites. As an example, \( S \) can represent the pixel positions of an \( m \times m \) image in a 2-D lattice \( \{(i,j) | 1 \leq i,j \leq m\} \) where the double indexing can be recoded to univariate indexing by \( (i,j) \rightarrow (i-1)m+j \) so that \( S=\{ 1,2,…,m^2 \} \).
The family \( X \) is called a Random Field.
Assume each \( X_i \) takes values \( x_i \in L\). \( L \) can be some label set.
E.g if \( L =\{0,1\} \), then \(P(X_1=x_1,X_2=x_2)=P(X_1=0,X_2=1)\) when \(x_1\) is 0 and \(x_2\) is 1.
To make notations simple, lets write \( P(X_i=x_i)\) as \(P(x_i)\), and the joint probability \( P(X_1=x_1,…,X_n=x_n) \equiv P(x_1,…,x_n) \equiv P(\textbf{x}) \).
\(\textbf{X}\) is called a Markov Random Field (MRF) on \(S\) with respect to a neighborhood system \(N\) iff the following holds:
- \(P( \textbf{x} ) > 0\) for all \( \textbf{x} \in \Xi \) where \(\Xi\) has all possible configurations assignment values of the \(n\) random variables \(X_1,X_2,…,X_n \),and,
- Markovianity property, i.e,
e.g for the network or graph below:
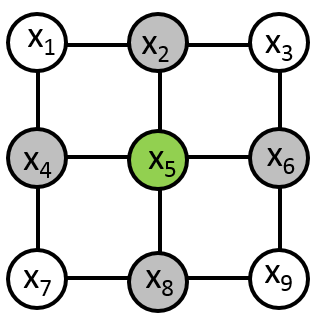
The neighbors of node \(x_5\) are \(x_2,x_4,x_8,x_6\). So \(N(x_5)=\{x_2,x_4,x_8,x_6\} \).
Then \(P(x_5 \vert x_1, x_2, x_3, x_4, x_6, x_7, x_8, x_9)\) = \( P(x_5 \vert x_2, x_4, x_8, x_6) \).
The conditional probability of a node given its neighbors \(P(x_i \vert N(x_i))\) is given by:
\[\begin{align} P(x_i \vert N(x_i)) & = \dfrac {P(x_i,N(x_i))} {\Sigma_{x_i \in L} P(x_i,N(x_i)) } \\\\ & = \dfrac {P(x_i,N(x_i))} {P(X_i=0,N(x_i))+P(X_i=1,N(x_i)) } \end{align}\]when, for example, \( L =\{0,1\} \).
References
TBA.
